Why Graphene material of the future ?!!

Why Graphene material of the future ?!!
1- Strength :
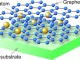
The secret lay in graphene atomic building it an abundant mineral which is an allotrope of carbon that is made up of very tightly bonded carbon atoms organised into a hexagonal lattice very thin atomic thickness (of 0.345Nm).
So it expects to see graphene used as a layer in bulletproof vests, armor, aircraft skin, etc., and certainly not replacing copper flashing on roofs, cladding on cookware, etc.
2- Electronics :

Graphene bulletproof can stop bullet easily because graphene 200 times stronger than steel
3- Safety:
This strength leads to Recent tests suggest that pure graphene performs twice as well as the fabric currently used in bulletproof vests, making it an ideal armour for soldiers and police, Professor Jae-Hwang Lee at the University of Massachusetts-Amherst devised a new miniature ballistics test to test graphene’s mettle. They used a laser pulse to superheat gold filaments until they vaporised, acting like gunpowder to fire a micrometre-size glass bullet into 10 to 100 sheets of graphene at 3 kilometres per second – about three times the speed of a bullet fired from an M16 rifle.
Researchers have been studying graphene as armour for some time, but Lee’s is the first paper to describe just how the material absorbs kinetic energy. Sound waves travel three times faster through graphene than they do through steel, which means material far beyond the impact point can quickly absorb and dissipate its energy – effectively slowing the projectile down and helping prevent its penetration. What’s more, the micro bullet methods Lee developed could be used to study other high-performance materials in extreme conditions.
4- Power :
5- Electricity :

Graphene plane will have super features and use less fuel
6- Mechanics :
Graphene Roll Up to make Carbon NanoTubes (CNTs) and it enter in a lot of fields
7- Nanotechnology:
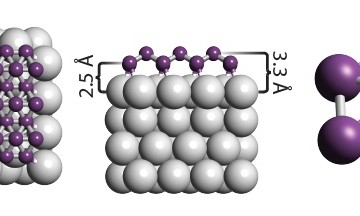
Graphene will replace copper in nano sutures because electrical resistance in 40-nanometer-wide nanoribbons of epitaxial graphene changes in discrete steps. The ribbons’ conductance exceeds predictions by a factor of 10. The ribbons can act more like optical waveguides or quantum dots, allowing electrons to flow smoothly along the ribbon edges. In copper, resistance increases in proportion to length as electrons encounter impurities.